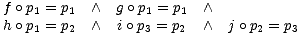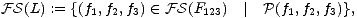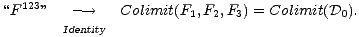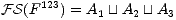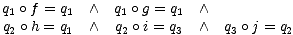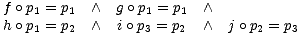
A Limit-Form for the diagram D is an optimal¹²

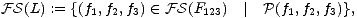
solution of this equation system. One such optimal solution L is explicitly given as follows: where the maps p₁, p₂ and p₃ are the natural projections from the cartesian product FS(F₁₂₃) = A₁ × A₂ × A₃ to its three factors.

In our heuristic we associate the dual construction of a Colimit-Form for a diagram like D with the activity of an idealized modelist. His main activity consists in gluing objects. He may do so on the denotator-level as well as on the formal level. The global object obtained from the four Euler-Tone-Net-Maps (cf. section 1) is a typical example for such an activity on the denotator level.¹³

Another type of gluing things is classification. This is what happens in a Colimit-Form construction. Our idealized modelist starts by studying the Coproduct

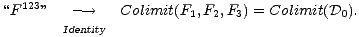
Its FrameSet is the disjoint union

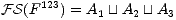
In his further activity he aquires the ability to identify those F¹²³-denotators with each other that are connected by one of the set-maps in the diagram D. He thus turns the predicate P into a system of equations for Forms

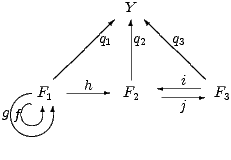
The variable Form Y of this system of equations involves three variable set-maps q_i : A_i FS(Y ) i = 1,2,3 from the AmbientSets of F₁, F₂ and F₃ into the FrameSet FS(Y ) of Y and the equations read as follows:

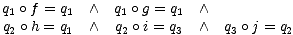
A Colimit-Form for the diagram D is an optimal solution for this system of equations. One such optimal solution C is explicitly given in terms of the FrameSet