3 Birkhoff’s Aesthetic Measure.
George David Birkhoff (1884-1944) who worked brilliantly on the three body problem, differential equations, general relativity among other areas and was an honorary member of the Mathematical Society of México, and who contributed also to the cultural development of México. In 1924 he retakes some ideas (see also Birkhoff, 1929, 1932, 1933, 1945) he had several years before, but which he did not develop because he had to focus on pure mathematics studies. (Sounds familiar?) He thought that the melody depended on the order of the notes as heard by the ear. He thought that certain order relations could be established, kept by the notes, so to choose the best melodies. For him, the Fundamental Problem of Aesthetics was to determine, for a class of objects, the specific characteristics on which the aesthetic value depends.
Birkhoff considers that there are three consecutive phases for the aesthetic experience: first, a preliminary effort of attention, which is necessary to perceive an object and that is proportional to the complexity  of the object; second, a pleasurable sensation or aesthetic measure
of the object; second, a pleasurable sensation or aesthetic measure  which rewards the preliminary effort; and third, a certification that the object possesses a harmony, symmetry or order
which rewards the preliminary effort; and third, a certification that the object possesses a harmony, symmetry or order  which seems to be a necessary condition, if not sufficient, for the aesthetic experience. So, Birkhoff proposes the formula
which seems to be a necessary condition, if not sufficient, for the aesthetic experience. So, Birkhoff proposes the formula 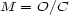 with which he expresses the aesthetic measure as the effect of the density of the order relations compared to complexity. He inquires the daring of the formula and provides certain historical justifications. Aesthetics deal with aesthetic pleasure and with the objects that produce it. So, we have classes of objects that can be compared with respect to their aesthetic value (objects in different classes can not be compared). Then, the fundamental problem of analytic aesthetics is to determine the aesthetic factors and their relative importance. To perceive an aesthetic object requires certain adjustments, and the effort sensation or tension that goes with it appears as the sum of all tensions to the diverse automatic adjustments. So, if
with which he expresses the aesthetic measure as the effect of the density of the order relations compared to complexity. He inquires the daring of the formula and provides certain historical justifications. Aesthetics deal with aesthetic pleasure and with the objects that produce it. So, we have classes of objects that can be compared with respect to their aesthetic value (objects in different classes can not be compared). Then, the fundamental problem of analytic aesthetics is to determine the aesthetic factors and their relative importance. To perceive an aesthetic object requires certain adjustments, and the effort sensation or tension that goes with it appears as the sum of all tensions to the diverse automatic adjustments. So, if 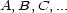 represent the adjustments, each with tensions
represent the adjustments, each with tensions  and if these are realized
and if these are realized 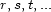 times, he considers the sum
times, he considers the sum  as the complexity.
as the complexity.
From another side, to the order  correspond certain associations that intervene in the act of perception. For example, symmetry would be an association. If
correspond certain associations that intervene in the act of perception. For example, symmetry would be an association. If  are associations of various kinds, each one with index of sensation
are associations of various kinds, each one with index of sensation  which happens
which happens  times, then we can consider the total of sensations (positive or negative)
times, then we can consider the total of sensations (positive or negative)  as the order of the object. Hence, the intuitive estimation of the quantity of order
as the order of the object. Hence, the intuitive estimation of the quantity of order  inherent to the aesthetic object, compared to its complexity, yields us its aesthetic measure. Obviously, this mathematical theory can only apply to objects whose aesthetic factors are essentially mathematical or formal. There are other factors that are beyond this theory, as for example, the associations about the signification of a beautiful poem. Birkhoff enumerates how some thinkers have perceived the presence of mathematical elements in art. It is interesting to see what they thought.
inherent to the aesthetic object, compared to its complexity, yields us its aesthetic measure. Obviously, this mathematical theory can only apply to objects whose aesthetic factors are essentially mathematical or formal. There are other factors that are beyond this theory, as for example, the associations about the signification of a beautiful poem. Birkhoff enumerates how some thinkers have perceived the presence of mathematical elements in art. It is interesting to see what they thought.
In contrast to the hedonistic, mystic or moralist theories, the analytic theory concentrates in providing a quantitative solution to the fundamental problem mentioned above. It would seem that aesthetics, if it has to be considered scientific, has
 of the object; second, a pleasurable sensation or
of the object; second, a pleasurable sensation or  which rewards the preliminary effort; and third, a certification that the object possesses a harmony, symmetry or
which rewards the preliminary effort; and third, a certification that the object possesses a harmony, symmetry or  which seems to be a necessary condition, if not sufficient, for the aesthetic experience. So, Birkhoff proposes the formula
which seems to be a necessary condition, if not sufficient, for the aesthetic experience. So, Birkhoff proposes the formula 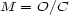 with which he expresses the aesthetic measure as the effect of the density of the order relations compared to complexity. He inquires the daring of the formula and provides certain historical justifications. Aesthetics deal with aesthetic pleasure and with the objects that produce it. So, we have classes of objects that can be compared with respect to their aesthetic value (objects in different classes can not be compared). Then, the fundamental problem of
with which he expresses the aesthetic measure as the effect of the density of the order relations compared to complexity. He inquires the daring of the formula and provides certain historical justifications. Aesthetics deal with aesthetic pleasure and with the objects that produce it. So, we have classes of objects that can be compared with respect to their aesthetic value (objects in different classes can not be compared). Then, the fundamental problem of 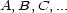 represent the adjustments, each with tensions
represent the adjustments, each with tensions  and if these are realized
and if these are realized 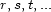 times, he considers the sum
times, he considers the sum  as the complexity.
as the complexity.  correspond certain associations that intervene in the act of perception. For example, symmetry would be an association. If
correspond certain associations that intervene in the act of perception. For example, symmetry would be an association. If  are associations of various kinds, each one with index of sensation
are associations of various kinds, each one with index of sensation  which happens
which happens  times, then we can consider the total of sensations (positive or negative)
times, then we can consider the total of sensations (positive or negative)  as the order of the object. Hence, the intuitive estimation of the quantity of order
as the order of the object. Hence, the intuitive estimation of the quantity of order  inherent to the aesthetic object, compared to its complexity, yields us its aesthetic measure. Obviously, this mathematical theory can only apply to objects whose aesthetic factors are essentially mathematical or formal. There are other factors that are beyond this theory, as for example, the associations about the signification of a beautiful poem. Birkhoff enumerates how some thinkers have perceived the presence of mathematical elements in art. It is interesting to see what they thought.
inherent to the aesthetic object, compared to its complexity, yields us its aesthetic measure. Obviously, this mathematical theory can only apply to objects whose aesthetic factors are essentially mathematical or formal. There are other factors that are beyond this theory, as for example, the associations about the signification of a beautiful poem. Birkhoff enumerates how some thinkers have perceived the presence of mathematical elements in art. It is interesting to see what they thought.