|
It began around a couple of decades ago. One of the main goals of Mathematical Music Theory is to develop a scientific framework for musicology. This framework has established scientific fields as foundation. It includes a formal language for musical and musicological objects and relations. Music is fundamentally rooted within physical, psychological and semiotic realities. But the formal description of musical instances corresponds to mathematical formalism. This theory is based on the theories of modules and categories, algebraic and combinatorial topology, algebraic geometry, representation theory, i.e., on heavy mathematical machinery. Its purpose is to describe the musical structures. The philosophy behind it is understanding the aspects of the music that are susceptible to the reason in the same way as physics does it for natural phenomena. This theory is based: in an appropriate language in order to manage the relevant concepts of musical structures, in a group of postulates or theorems with regard to the musical structures subject to the defined conditions and in the functionality for the composition and the analysis with or without computer. Mazzola, in his magnificent panoramic article Mazzola (1998), cites Boulez’ elements of a program of the sixties, which aims at realizing imagination such that arts and science are effectively reconciled. (I should add, artists and scientists). In this postulate, Boulez’ invocation of the »royal imagination« can only be envisaged by the virtual (essential) realization of the complex theoretical as well as practical system of music, its sounds and their relations by means of today’s information technology. Mazzola continues: »Music is a central issue in human life-thought, it affects another layer of reality than physics. We believe that the attempt to understand or to compose a major work of music is as important and difficult as the attempt to unify gravitation, electromagnetism, weak, and strong forces.« »For sure, the ambitions are comparable, and hence, the tools should be comparable, too.« Mazzola agrees with Boulez in that, »music can not be degenerate or reduced to a section of mathematics: music is fundamentally rooted within physical, psychological and semiotic realities. But we need more sophisticated methods besides statistical and empirical data in order to formally describe musical instances.« In the eighties Mazzola observed that the musical structures were global structures glued from local data. Mazzola used the selection of a cover as atlas, which is part of the point of view in the sense of Yoneda and Adorno. The charts are called local compositions and they consist roughly of finite subsets Mazzola mentions three major paradigms of mathematics and musicology that have occurred during the last 150 years and that have paralleled the evolution of both and the increasing presence of mathematics in musicology. Those are: global gestalts or structures, symmetries and the Yoneda philosophy.
|
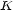 of modules
of modules  over a ring
over a ring 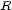 . These charts
. These charts  are glued and compared by means of isomorphisms of the underlying modules. Such global objects, which generate different categories, are called
are glued and compared by means of isomorphisms of the underlying modules. Such global objects, which generate different categories, are called