polygonal forms, to ornaments and to pots.

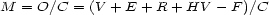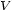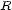For the case of the aesthetic measure of polygonal forms, Birkhoff considers the formula where is the vertical symmetry, is the equilibrium, is the central symmetry, is the relation with a horizontal-vertical net, 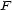is the non-satisfactory form that includes several factors, and is the complexity. Each variable assumes values depending on several conditions, too long to enumerate here. He also applies his formula to diatonic chords, harmony and melody, as well as to musical quality in poetry.

In the musical case, his theory is based in the order relations between notes, and since the appreciation of such relations continuously changes and develops, he tries not to form a definitive theory of aesthetic measure that is valid for the future or the past. He considers that the principal problem of the musical form is that given a set of musical resources we must determine to what extent the order relations between the notes of a composition constitute an efficient basis for musical delight.

For the diatonic chords, the complexity 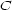is left apart, since a simple chord is a unitary object and the only automatic adjustments are incipient ones to a single set of notes, so the aesthetic measure of a chord would be equal to its order. Then where is the aesthetic measure of a single chord, taken in a major tonality or key for example, 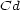denotes the value of a chord and refers to certain invariant characteristics that do not change when its superior notes move upward or downward by octaves, is the value of the interval and 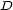is the value of the dominant note. In the case of chord progression, Birkhoff proposes the formula 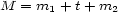where 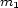and 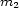denote the aesthetic measure of the chords and the transition.

Birkhoff also analyzes the melody problem but leaves open the rhythm problem. His work can be continued even further, and the use of computers would be of great help. His intention was to provide systematic procedures of analysis in simple domains of aesthetics. He concludes that there is an enormous difference between the discovery of a diamond and its appraisal, even further, between the creation of a work of art and an analysis of the formal factors that intervene in it.

4 Fibonacci Numbers and Bartók.

In 1202 Leonardo de Pisa, whose nickname was Fibonacci (in abbreviation of filius Bonacci) wrote a book called »Liber Abacci« (or book about the abacus). We have the second edition of 1228. It contained almost all arithmetic and algebraic knowledge of that time and played a fundamental role in the development of Western mathematics, since through it, the Europeans got familiarized with the Indo-Arab numerical system. It contained lots of examples. Let us see one of them reformulated in the following way: Suppose that the rabbits do not reproduce during their first month of life, but that from the second month on, each couple produces a new pair. Suppose that no rabbit dies. If we start with a pair of rabbits, how many pairs of rabbits are there after 12 months and in general after months? The sequence of adult pairs is of the form