|
that is, the sequence given by the formula 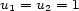 and and  for for  greater or equal to greater or equal to  . This sequence is called Fibonacci sequence and its terms Fibonacci numbers. If we consider . This sequence is called Fibonacci sequence and its terms Fibonacci numbers. If we consider  as the growth coefficient, we will obtain a sequence, whose limit when as the growth coefficient, we will obtain a sequence, whose limit when  tends to infinity is tends to infinity is  . . This number plays a very important role in geometry and aesthetics. If we divide a segment of a line Bela Bartók (1881-1945) around 1915 developed a method to integrate all the elements of music (scales, structures of chords with the appropriate melodic motives, proportions of length, so much of the work in general as those of the exposition, development, reexposition or recapitulation, connection phrases among movements, etc.) based on the golden section (c.f. Lendvai, 1979). It is surprising that Bartók never wrote or spoke of this during his life. The Chaldeans had already intended to use the golden section as an aesthetic principle 3000 years BC, the Greeks used it 2000 years after them and it was reused in the Renaissance but never in music. Only a movement of a quartet from Haydn is known, composed in agreement to the golden section in its length, but this is rather an isolated composition than a principle or composition method. The tonal circle of Bartók is the following. Consider the circle of neighboring tonalities or circle of fifths in the following way: make a one-to-one correspondence among the notes {do, do#, re, re#, mi,..., si} or {c, c#, d, d#, ..., b} and the numbers As for the form and the harmony, Bartók uses the principle of the golden section. For example, in the first movement of the »Sonata for Two Pianos and Percussion«, which consists of 443 bars, if one multiplies this number by 0.618... the bar 274 is obtained, which will be the center of gravity of the movement. In this way, the reexposition or recapitulation occurs in bar 274. Similarly it happens to the first movement of »Contrasts«, which consists of 93 bars, number that if multiplied by 0.618... gives the bar 57, where the reexposition or recapitulation begins. There are many more examples. As for the harmonic treatment, from bars 2 to 17 of the introduction of the »Sonata for Two Pianos and Percussion« is where they the germs of the work are settled. The bars 2 to 5 of the first part are in the tonic F#-C with the motive in fundamental position, the bars 8-9 of the second part are in the dominant G-D |
 in a point
in a point 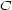 such that
such that  , such a quotient is called
, such a quotient is called 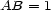 and
and 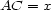 , then
, then 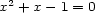 . So
. So  . In this way, the bigger part of any length, divided by the golden section is equal to the total length multiplied by
. In this way, the bigger part of any length, divided by the golden section is equal to the total length multiplied by  .
. 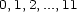 in that order; then, consider the cyclic group
in that order; then, consider the cyclic group 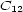 generated by
generated by  and order this group in a circumference. Let us take the c like the tonic T and assign the letters D, S and T successively to each note of the circle. D will designate the
and order this group in a circumference. Let us take the c like the tonic T and assign the letters D, S and T successively to each note of the circle. D will designate the 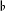 also with the motive in fundamental position and the third part, from bar 12 on is in the subdominant A
also with the motive in fundamental position and the third part, from bar 12 on is in the subdominant A -D with the inverted motive. There are 46 units of value
-D with the inverted motive. There are 46 units of value